La media aritmética. Qué es y cómo se usa

Una de las dimensiones del análisis estadístico más importante es la evaluación del centro de datos; pues allí es donde se supone que se agrupa la mayor cantidad de los datos; se dice que hay densidad de datos y, por lo tanto, funciona como un atractor de estos. Las medidas usadas para la evaluación del centro son, la media, la mediana y la moda. Las tres son muy importantes y no deberían despreciarse. En esta ocasión hablaremos de la media.

Intuitivamente, es decir, el sentido que tiene esta medida, es que es el punto de equilibrio de la distribución; esto es, reparte los “pesos” o cargas alrededor de ella. En la figura A, la balanza romana equilibra o reparte las cargas de las frutas y del peso, estableciendo así la equivalencia entre estos. En la figura B, la gimnasta parece extender más cuerpo de un lado que de otro, respecto del apoyo; pero no es así, lo que está equilibrando es el peso en ambos lados.

A. Balanza romana

B. Gimnasta

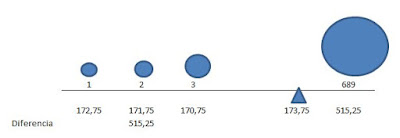
Eso hace la media, equilibra las cargas. ¿qué significa esto respecto de los valores? En la tabla siguiente podemos ver cuatro valores (1, 2, 3, 689), tres de ellos consecutivos y el cuarto valor muy extremo respecto de estos. Al obtener la media nos da 173,75. Observemos que los tres valores a la izquierda de la media son, individualmente, menores que el valor de la derecha; sin embargo, si obtenemos las diferencias entre estos y la media, y luego las sumamos, nos dará el mismo valor a la diferencia entre la media y el valor mayor. Esto es, (173.75 – 1) + (173.75 – 2) + (173.75 – 3) = (689 – 173.75); en ambos casos nos da 515.25. A estas diferencias es a lo que nos referimos como cargas.

Veamos esto con más detalle. La media no de "fija" en los valores individuales, como 1,2,3 y 689; sino en la diferencia que tienen estos respecto de ella; es decir (173.75 – 1) = 172,75 es la primera carga que sopesa la media;  (173.75 – 2) = 171,75 es otra carga;  (173.75 – 3) = 170,75 es la tercera carga del lado izquierdo y (689 – 173.75) = 515,25 es la carga del lado derecho de la media. Es decir lo que sopesa la media son estas cargas. Puede verse que 172,75+171,75+170,75 = 515,25 dando igual que la carga de la derecha de la media. Por ello decimos que la media sopesa las cargas, es el punto de equilibrio de la distribución. Por otra parte la mediana si se "fija" en los valores (no en las cargas) y se coloca en medio de estos.
Esto es lo que distribuye la media; ella se coloca en el lugar justo donde equilibra las cargas, esto es en 173.75. por ello se dice que la media es el valor que deberían tener todos los valores si fuesen iguales.

Ahora, ¿qué significa la media en términos de su cálculo? Mas allá de su cálculo automático, la media es el resultado de dos procesos significativos; el primero es la agregación de los valores a través de la suma, y el segundo la división de esta suma, o masa de datos agregada, entre el total de valores agregados. Esto tiene varios significados, el primero es que en la media participan todos los valores, a diferencia de la mediana y de la moda. Con ello se dice que la media contiene toda la información de los datos. Una vez obtenido ese total o masa de datos agregados, se dividen en partes proporcionales según el numero de valores agregados. Por ello se dice que la media es el valor que deberían tener todos los valore si fuesen iguales; pero no lo son, por lo que la media es un valor de referencia

Usos de la media

Ahora nos preguntamos ¿Cuándo usar la media? Generalmente se dice de ella que es el valor justo de las cosas ¿será cierto? Supongamos que el condominio de un edificio de 5 apartamentos ofrece pagar el consumo de gas doméstico usando la media; supongamos que los consumos son: 45, 47, 135, 39 y 58. Siendo la media 64,8 ¿sería justo que todos pagaran la media de consumo? Claramente los que consumen menos que la media tendrían que pagar más; por lo tanto, la media no siempre es un valor justo. Igualmente sucede con los salarios o con los precios. En parte esto se resuelve a través de la media ponderada, esto es agregarle al valor que se va a promediar un ponderador que iguale la importancia de cada uno. Por ejemplo, sacar un 16 en matemática es igual a sacarlo en lengua, pero seguramente ambas asignaturas habrán requerido de esfuerzos y habilidades distintas; es por esto que las notas de matemáticas se ponderan más que las de lengua; esto es se les da un valor distinto, por ejemplo 6 a matemática y 4 a lengua, por lo tanto, las notas individuales han de ser ponderadas por el valor de cada asignatura. Este asunto del valor de las cosas no tiene que ver directamente con la media; lo que se dice es que se cae en errores si se obtiene la media simple o aritmética si no se tiene en cuenta las ponderaciones de las cosas. La media es más útil si se aplica poblaciones homogéneas, del mismo tipo o que comparten similares características estadísticas, también se dice que están en estratos similares.

Matemáticamente la media ofrece bondades muy importantes por lo que se la escoge para trabajar con las funciones de probabilidad; de este modo su uso en probabilidades es necesario. Finalmente expresar que, para evitar conclusiones apresuradas en la interpretación de la media, es aconsejable que se obtengan otros estadísticos para valorar la media dentro de la masa de datos.